https://atticus262.tistory.com/80
망상은 망상에서 머물러야 하는 법이다. 역시나 쓸데없는 걸 쓰기 시작했다는 반성은 하고 있다. 지난 포스팅은 롤라이35의 피사계 심도를 나타낸 표를 보며 생겨난 궁금증에서 비롯됐다. 그렇게 시작한 지적 여정은 촬상면에서의 착란원 크기, 허용착란원의 소개, 롤라이35 제조사가 내세운 in-focus 의 기준까지 이어졌다. 이 기준이 믿을만 한 것인지 터무니없는 것인지를 살펴보려면, 허용착란원의 크기를 결정하는 '일반적 기준'에 대해 고려해야 할 필요가 생긴다. 오늘의 토론은 이 지점에서부터 출발한다.
허용착란원의 일반적인 기준은 풀프레임 규격에서 0.03, APS-C 규격에서 0.018이라고 알려져 있다. 물론, 촬상면 위에서 측정한 착란원의 한계 지름(mm)을 의미한다. 이보다 작은 모든 착란원을 사람은, '점'으로밖에 인식하지 못한다. 왜 하필 이 숫자들일까. 대체 어디에서 튀어나온 걸까. 이 부분의 논의는 또다른 티스토리 블로그 '럽의 세상담기'의 내용을 전적으로 참고한 것임을 미리 밝혀둔다.
http:// 출처: https://lovepoem.tistory.com/816 [럽의 세상담기]
일단, 사람이 그 눈의 최대 능력을 발휘해 사진을 보는 상황을 가정할 필요가 있다. 사진은 가까이서 볼수록 잘 보이기는 하지만, 우리 눈에도 카메라 렌즈처럼 '최소초점거리'라는 게 있다. 생물학에서 배운 '명시거리'의 개념대로라면, 사람은 25cm 떨어진 물체를 가장 자세히 들여다볼 수 있고, 이보다 가까워지면 오히려 초점을 정확하게 맞추기 어렵다. 명시거리가 존재한다는 점은 생물학의 명제이지만, 25cm라는 숫자는 학계에서 준용되는 실험적 통계라는 점을 고백한다. 그런 통계가 하나 더 있는데, 이 거리에서 사람이 크기의 변화를 감지할 수 있는 원의 최소 크기는 0.2mm라고 한다. 그보다 작은 원은, 점이든 원이든 다 똑같아보일 뿐이다.
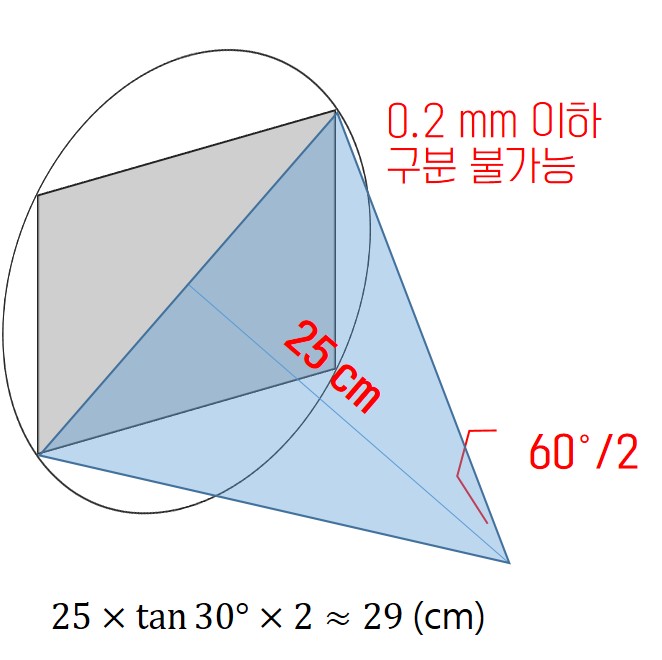
그렇게 했을 때 우리 눈의 화각이 약 60도라는 점을 기억하자. 나도 정확히는 모른다. 그렇다고 한다. 이런 상황이라면 25cm 떨어진 지름 29cm의 동그란 영역을 관찰하는 것이 우리 시력의 최선이라고 할 수 있다. 우리 시야의 원 내부에 집어넣고 볼 수 있는 가장 큰 사진이라면 대각선 길이가 역시 29cm라야 한다는 결론이다. 카메라 내부에서 상이 맺히는 촬상면은 분명 이 사진과 닮은 직사각형일 것이다. 그 대각선 길이 사이의 비율을 알면, 사진에서 우리가 '점'으로 인정해주는 최대 크기의 원이, 확대 인화되기 전 필름에서는 어느 정도 사이즈였는지를 알아낼 수 있다.
풀프레임 센서의 크기는 135포맷 필름과 같으므로, 35 mm × 24 mm 이다. 대각선의 길이는 피타고라스 정리를 이용해 쉽게 구할 수 있다. 이 길이가 290mm 가 되려면 약 6.83배 확대가 필요하다는 계산이 나온다. 이 정도면 확대 인화된 사진은 약 9" × 6" 크기보다 살짝 클 것 같다. 풀프레임 센서 혹은 필름 위의 어떤 착란원이 역시 그만큼 확대되었을 때 0.2mm 이하가 되어야 한다. 이 부등식을 풀면, 풀프레임에서 허용착란원의 크기는 0.029mm, 즉 약 0.03mm라는 답이 도출된다. 촬상면의 가로 길이가 36mm라고 해도 결과는 거의 똑같다.
같은 계산방식을 APS-C 센서에도 적용해볼 수 있다. 이 때 촬상면의 크기는 24 mm × 16 mm이다. 역시 피타고라스 정리를 이용해 구한 이 직사각형의 대각선의 길이는 10배가 되어야 290 mm에 이를 수 있다. 확대 인화된 사진 위의 0.2 mm 짜리 원이 사실은 센서에서 10배 커진 결과라는 뜻이다. 따라서 APS-C 센서에서 0.02 mm보다 작은 원은, 사람이 가장 잘 볼 수 있는 크기의 사진으로 확대 인화되더라도 점으로만 보인다는 뜻이 된다. 즉, 선명한 초점의 기준인 허용착란원이 APS-C 규격에서는 0.02 mm 라는 결론을 얻게 된다.

롤라이35의 설계자들은 15" × 10" 사진에서 0.25 mm 를 circle of confusion으로 정했는데, 같은 필름 크기를 가정한 일반적인 기준에서는 9" × 6"보다 약간 큰 사진 위에서 0.2 mm 를 한계로 보았다. 0.25가 0.2가 되기 위해서는 80% 크기로 축소되어야 하는데, 가로 길이만 비교해 봐도 보통의 관점에서 설정한 대각선 290 mm짜리 사진의 가로 길이가 12"에 이르지는 않는다. 굳이 비교하면, 롤라이 쪽이 더 엄격한 기준을 설정한 셈이 된다.
한 가지 재미있는 점은, 이런 허용착란원의 기준을 가지고 있을 때 렌즈가 '나름 선명한' 초점을 잡아내는 피사계 심도 혹은 포커스 존을 수학적으로 계산해낼 수 있다는 사실이다. 이전 포스팅에서는 롤라이35의 operation manual에 등장한 표를 이용해 숫자를 넣어 계산했지만, 이제는 변수와 상수들을 설정해 '일반적인' 초점 영역을 구해낼 수 있다. 어렵지는 않다. 숫자로 했던 방식에서와 동일하다.

촬상면에 생기는 착란원의 크기 c는 초점거리(F)와 조리개(N), 초점을 겨냥한 거리(a)와 다른 배경의 거리(x)에 의해 결정된다고 소개한 적이 있다(#0). 전경의 경우는 피사체보다 가깝기 때문에 x-a가 음수가 되는데, 그렇다 하더라도 착란원의 크기는 0보다 작을 수 없기 때문에 절댓값 기호가 필요하다. 지난 포스팅에서 이 값들을 대입했던 것처럼 F=F, N=N, a=a, x=L일 때 착란원의 지름이 p라고 해보자(#1). 이 p가 점이라고 인정해줄 수 있는 최대 크기, 즉 허용착란원이라면, L은 아마도 피사계 심도의 끝점 중 하나가 될 수밖에 없다. L이 a보다 크면 L-a로 계산하고(왼쪽), L이 a보다 작은 경우(전경)에는 a-L로 계산해주면(오른쪽) 결과를 항상 양수로 만들어줄 수 있다. 그래서 언제나 가까운 L과 먼 L 두 가지 경우가 발생하게 된다. 지금부터 L을 구해보도록 하자.
우선 p를 양변에서 공평하게 나눠주자(#2). p가 우변의 분모로 이동하고 좌변은 통채로 1이 됐다. 여기서 중요. 표현의 편의를 위해서 (F*F)/(p*N) 을 h라고 표기해주도록 한다. 지금까지의 식을 h를 이용해 다시 표현해준다(#3). 양변에 (a-F)*L을 사이좋게 곱해주고(#4), L이 곱해진 항들과 그렇지 않은 항들을 좌변 우변으로 분리해준다(#5). L이 곱해진 대괄호로 양변을 나눠서 L을 얻는다(#6).
가까운 L과 먼 L의 식을 보면 분자는 모두 ha로 똑같다. 분모의 생김새도 대칭적인데, 한쪽은 (h-F) + a이고 다른쪽은 (h+F) - a이다. 여기서 만일 초점을 겨눈 거리 a가 h+F와 같아지면 어떻게 될까? 먼 L의 값이 무한대가 된다. 가까운 L부터 별나라까지도 모두 초점을 '정확히' 맺는다는 의미이다. 아까부터 (F*F)/(p*N)를 편의상 h라고 불러왔지만, 사실은 손쉬운 초점잡기와 관련된 힌트가 숨어 있다. h+F 만큼의 거리를 초점 맞출 거리(a)로 설정해놓고 돌아다니면, (h+F)/2부터 무한대까지는 모두 별다른 조작없이 초점을 맺게 할 수 있다. 이것을 과초점거리 라고 부른다.
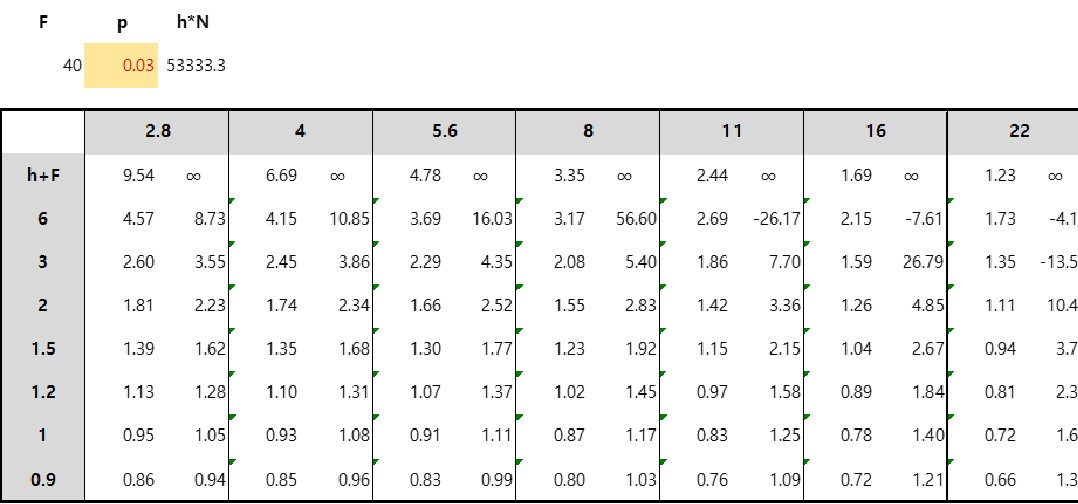
롤라이 나름의 기준으로 만들어진 포커스 존 표는 소개한 적이 있으니, 이번에는 허용착란원 0.03을 적용해 직접 표를 만들어보면 대략 다음과 같다. 간단히 비교해보면, 역시 롤라이에서 만든 표가 더 깐깐한 기준에서 태어난 것임을 확인할 수 있다. 즉, 더 정확하고 선명하게 맞은 초점이라야 '롤라이 기준'을 통과할 수 있다.
그런데, 착란원 크기를 계산하는 공식이 지난 번부터 왜 저렇게 생겼는지는 아무도 궁금해 하지 않으려나? ㅋㅋㅋㅋㅋㅋ
'사진가 > 촬영과 보정 연구' 카테고리의 다른 글
| 은하수 촬영 셔터속도 알려주는 NPF 공식 (2) | 2022.12.21 |
|---|---|
| 착란원(보케, 빛망울, 아웃포커스 효과) 크기 공식의 증명 또는 계산 (0) | 2020.12.31 |
| 롤라이35 조리개별 거리별 피사계심도, 허용착란원 기준 (4) | 2020.12.19 |
| 디지털사진 보정 이야기. 라이트룸을 추천하는 이유 (6) | 2020.11.30 |
| 카메라설정 RAW vs. JPEG, 떡보정과 원본순결주의 사이 (7) | 2020.11.23 |